오류역전파 알고리즘 프로젝트

[공지사항] 민혁 블로그 신규 포스팅 안내 드립니다.

[인공지능] 오류역전파 알고리즘 구현

< Backpropagation algorithm >

Backpropagation 알고리즘 설계 요소

• Python 언어 사용(numpy)
• 데이터셋, 특성(feature) 4개
• 총 데이터 개수 = 75개
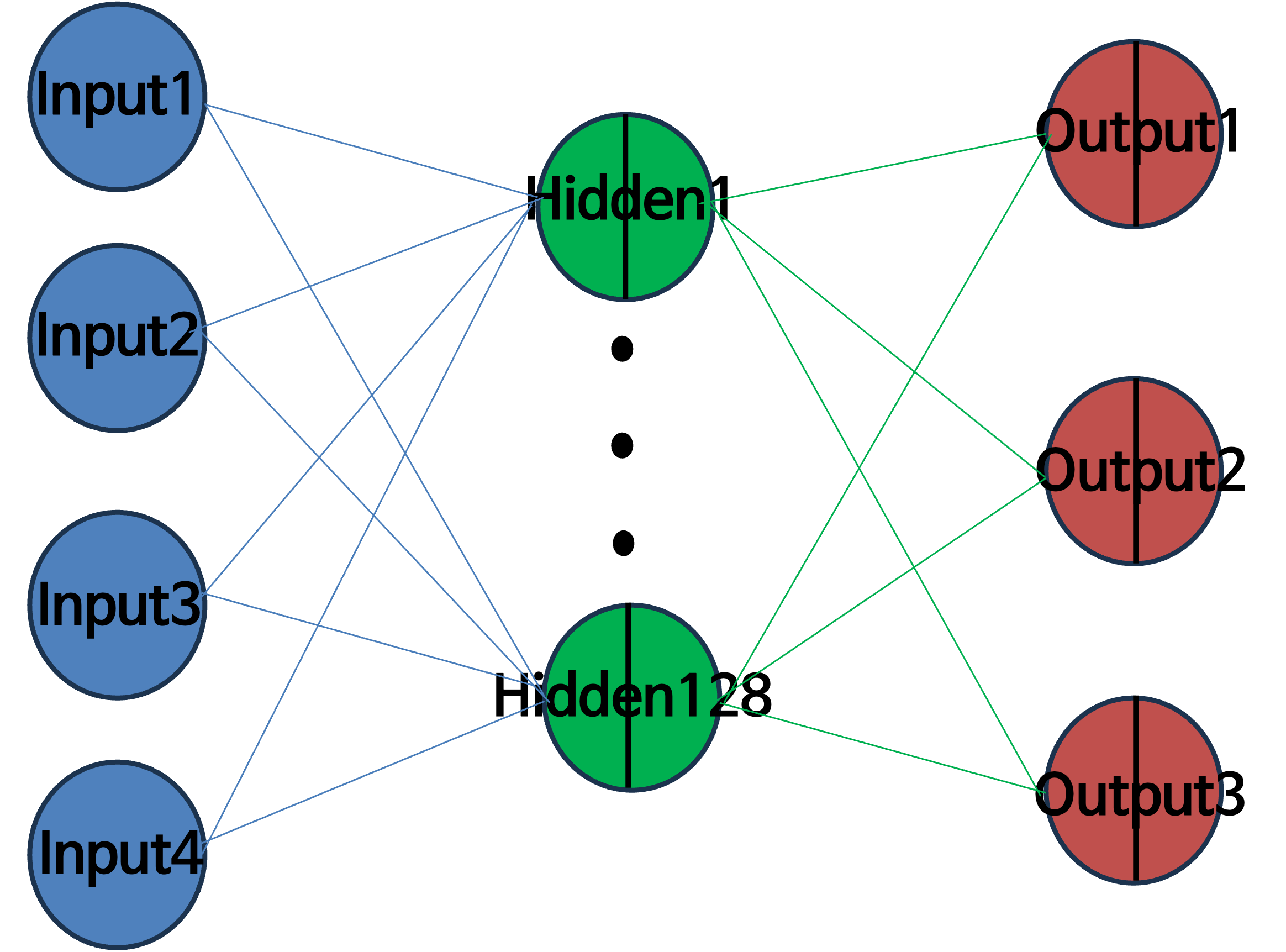
• 은닉층 1개
• 활성화 함수: sigmoid 함수, softmax 함수

---

코드 구현 순서

1. 데이터셋 분리, One-Hot Encoding
2. Parameter, 가중치 초기화 / 활성화 함수 및 학습 적용
3. 순전파 진행 / 손실 계산 / 역전파 진행 / 가중치, 분산 업데이트
4. 검증 데이터셋의 모델 평가 및 class 분류 나타내기

---

    import numpy as np

    # 파일 경로
    train_data_path = '/content/training.dat'
    test_data_path = '/content/testing.dat'

    # 데이터 로드
    train_data = np.loadtxt(train_data_path)
    test_data = np.loadtxt(test_data_path)

    # 데이터셋 분리(특성과 레이블)
    X_train = train_data[:, :-1]
    y_train = train_data[:, -1].astype(int)
    X_test = test_data[:, :-1]
    y_test = test_data[:, -1].astype(int)

    # 원-핫 인코딩
    classes = len(np.unique(y_train))
    y_train_encoded = np.eye(classes)[y_train]
    y_test_encoded = np.eye(classes)[y_test]

    # 모델 파라미터
    input_size = X_train.shape[1]
    hidden_size = 128  # 은닉층의 크기
    output_size = classes

    # 가중치 초기화
    np.random.seed(42)
    weights_input_hidden = np.random.randn(input_size, hidden_size)
    bias_hidden = np.zeros(hidden_size)
    weights_hidden_output = np.random.randn(hidden_size, classes)
    bias_output = np.zeros(classes)

    # 활성화 함수 정의(Sigmoid 함수 사용)
    def sigmoid(x):
        return 1 / (1 + np.exp(-x))


    learning_rate = 0.02  # 학습률

    epochs = 80000  # 학습 횟수(epoch) 80000번 반복

    # 모델 학습
    for epoch in range(epochs):
        # 순전파 진행
        hidden_input = np.dot(X_train, weights_input_hidden) + bias_hidden
        hidden_output = sigmoid(hidden_input)
        output_layer_input = np.dot(hidden_output, weights_hidden_output) + bias_output
        pred_scores = sigmoid(output_layer_input)

        # 손실 계산
        loss = np.sum((pred_scores -y_train_encoded) ** 2) / (2 * len(X_train))

        # 역전파 진행(경사하강법)
        output_error = pred_scores - y_train_encoded
        hidden_error = np.dot(output_error, weights_hidden_output.T) * hidden_output * (1 - hidden_output) # 활성화 함수의 미분

        # 가중치와 바이어스 업데이트
        weights_input_hidden -= learning_rate * np.dot(X_train.T, hidden_error) / len(X_train)
        bias_hidden -= learning_rate * np.sum(hidden_error, axis=0) / len(X_train)
        weights_hidden_output -= learning_rate * np.dot(hidden_output.T, output_error) / len(X_train)
        bias_output -= learning_rate * np.sum(output_error, axis=0) / len(X_train)

        # 1000번의 반복횟수 마다 손실 출력
        if (epoch + 1) % 1000 == 0:
            print(f"Epoch {epoch + 1}/{epochs}, Loss: {loss}")

    # 테스트 데이터에 대한 모델 평가 및 클래스 분류
    hidden_input_test = np.dot(X_test, weights_input_hidden) + bias_hidden
    hidden_output_test = sigmoid(hidden_input_test)
    output_layer_input_test = np.dot(hidden_output_test, weights_hidden_output) + bias_output
    pred_scores_test = sigmoid(output_layer_input_test)

    # 테스트 데이터에 대한 클래스 분류 결과 계산
    pred_classes_test = np.argmax(pred_scores_test, axis=1)
    actual_classes_test = np.argmax(y_test_encoded, axis=1)

    # 데이터 및 클래스 출력
    for i in range(len(X_test)):
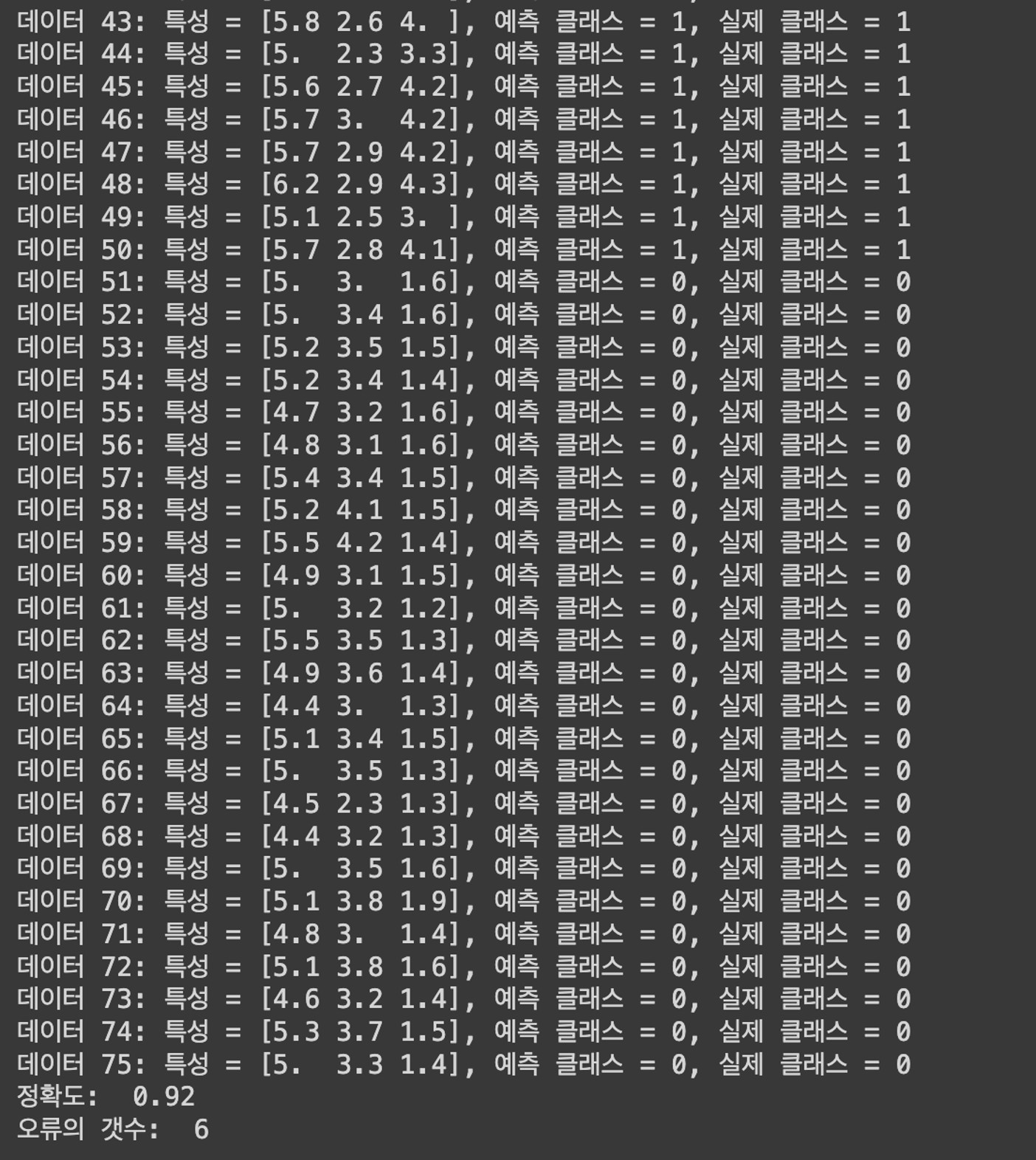
        print(f"데이터 {i + 1}: 특성 = {X_test[i]}, 예측 클래스 = {pred_classes_test[i]}, 실제 클래스 = {actual_classes_test[i]}")

    # 정확도 및 오류 출력
    errors_test = np.sum(np.not_equal(pred_classes_test, actual_classes_test))
    accuracy_test = 1 - errors_test / len(X_test)
    print("정확도: ", accuracy_test)
    print("오류의 갯수: ", errors_test)

학습 과정 및 결과

클래스 그래프

    import numpy as np
    import matplotlib.pyplot as plt

    # 파일 경로
    train_data_path = '/content/training.dat'
    test_data_path = '/content/testing.dat'

    # 데이터 로드
    train_data = np.loadtxt(train_data_path)
    test_data = np.loadtxt(test_data_path)

    # 데이터셋 분리 (특성과 레이블)
    X_train = train_data[:, :-1]
    y_train = train_data[:, -1].astype(int)
    X_test = test_data[:, :-1]
    y_test = test_data[:, -1].astype(int)

    # 그래프를 그리기 위한 데이터 포인트 생성
    colors = ['red', 'blue', 'green', 'purple']  # 클래스에 따른 색깔 지정
    markers = ['o', 's', 'D', '^']  # 클래스에 따른 마커 지정

    # 각 클래스에 해당하는 데이터 포인트 추출 및 그래프 그리기
    for class_label in np.unique(y_train):
        class_data = X_train[y_train == class_label]
        plt.scatter(class_data[:, 0], class_data[:, 1], label=f'Class {class_label}', color=colors[class_label], marker=markers[class_label])

    # 그래프 레이블 및 범례 추가
    plt.title('Class Distribution based on Features')
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.legend()
    plt.show()

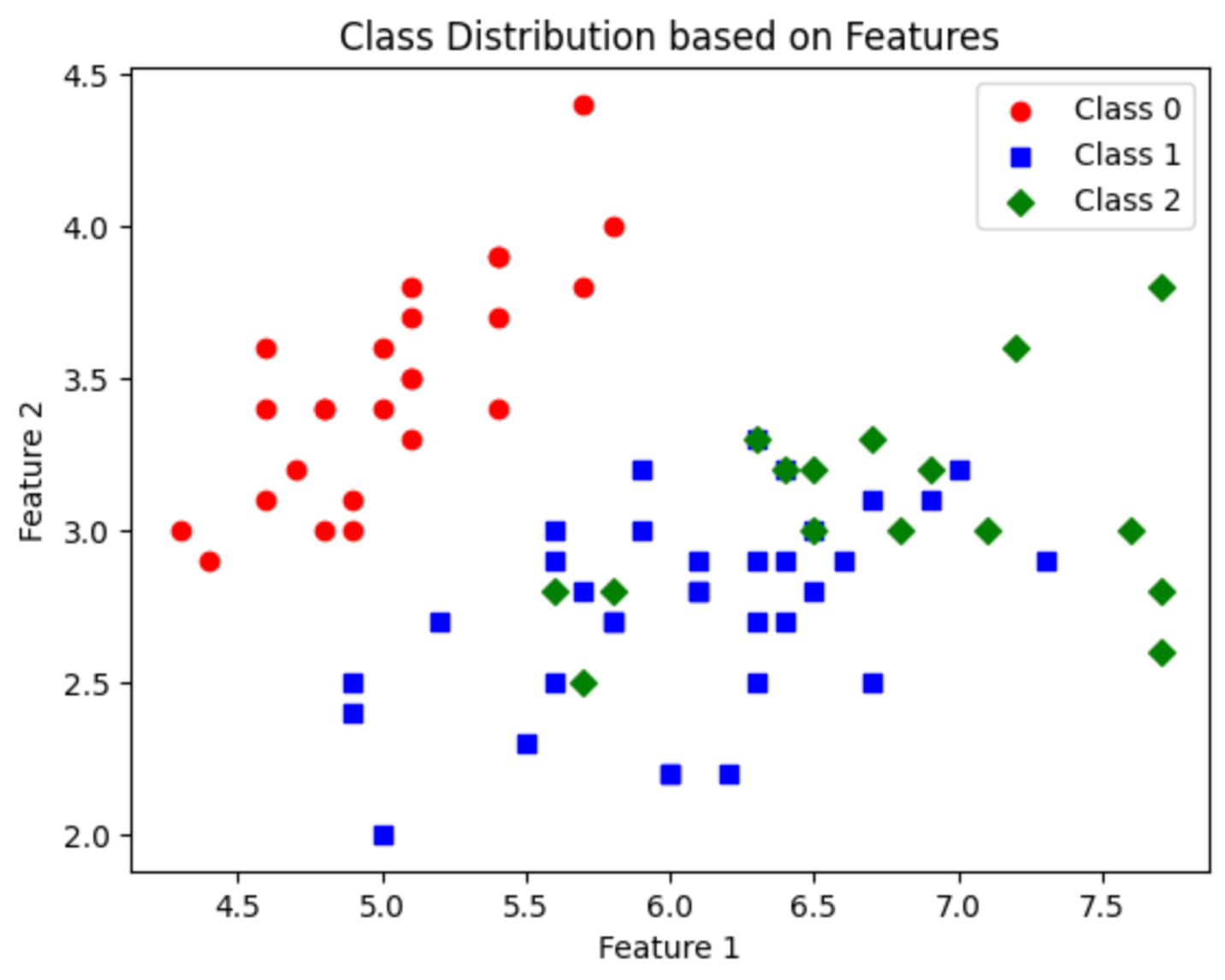
• 클래스 3개 (Class 0, Class1, Class 2)
• 정확도: 92%
• 오류의 개수: 6개 (시그모이드 – 92%, 6개) (시그모이드,소프트맥스 – 90%, 7개)